1 (page 161, # 26) Suppose that every member of
1 (page 161, # 26) Suppose that every member of
![]() has
cardinality at most
has
cardinality at most ![]() , then
, then
![]() .
.
Define
![]() by
by
![]() . If
. If
![]() and
and
![]() are two elements of
are two elements of ![]() with
with
![]() , then
, then ![]() and
and
![]() .
As
.
As ![]() is injective, we have
is injective, we have ![]() as well, so that
as well, so that ![]() . Thus,
. Thus, ![]() is injective showing that
is injective showing that
![]() .
.
Therefore,
![]() .
.
![]()
2 (page 161, # 27)
No. For ![]() a positive real number, let
a positive real number, let
![]() .
Then
.
Then ![]() is a circle and for
is a circle and for ![]() we have
we have
![]() . Set
. Set
![]() .
.
Yes. Recall that we defined a figure eight to be a set of the form ![]() where
where ![]() and
and ![]() are circles whose bounded disks meet at exactly one point. For
each pair of positive rational numbers
are circles whose bounded disks meet at exactly one point. For
each pair of positive rational numbers ![]() and
and ![]() with
with ![]() , we define
, we define
![]() to be the set of figure eights in
to be the set of figure eights in ![]() whose smaller circle has radius
whose smaller circle has radius ![]() with
with ![]() and whose large circle has radius
and whose large circle has radius ![]() with
with
![]() .
Note that
.
Note that
![]() is a countable union of the sets
is a countable union of the sets ![]() .
If we show that each
.
If we show that each ![]() is countable, then we know that
is countable, then we know that ![]() itself is.
Note that if
itself is.
Note that if
![]() are two distinct figure eights with the specified
conditions on their radii, then not only are
are two distinct figure eights with the specified
conditions on their radii, then not only are ![]() and
and ![]() disjoint, but the disks that
they bound are also disjoint as if
disjoint, but the disks that
they bound are also disjoint as if ![]() were a subset of the union of the disks
bounded by
were a subset of the union of the disks
bounded by ![]() , we would need the sum of the radii of the circles of
, we would need the sum of the radii of the circles of ![]() to be
less than the radius of the larger circle of
to be
less than the radius of the larger circle of ![]() , but this sum is at least
, but this sum is at least ![]() .
Thus, exactly as in part (a) we may define an injective function
.
Thus, exactly as in part (a) we may define an injective function
![]() showing that
showing that ![]() is countable.
is countable.
3 (page 161, # 28) Find a set
![]() of open intervals in
of open intervals in
![]() such that every rational number belongs to one of those
intervals but
such that every rational number belongs to one of those
intervals but
![]() .
.
Let
![]() .
.
4 (page 161, # 29) Let ![]() be a set of positive real numbers. Assume that there is a bound
be a set of positive real numbers. Assume that there is a bound ![]() such that the sum
of any finite subset of
such that the sum
of any finite subset of ![]() is less than
is less than ![]() . Show that
. Show that ![]() is countable.
is countable.
5 (page 161, # 30) Assume that ![]() is a set with at least two elements. Show that
is a set with at least two elements. Show that
![]() .
.
We break the argument into two cases at this point.
If ![]() is finite, then
each of the sets
is finite, then
each of the sets ![]() is also finite and, thus, at most countable. Therefore,
is also finite and, thus, at most countable. Therefore,
![]() is also at most countable. However, as
is also at most countable. However, as
![]() , we see that
, we see that
![]() .
.
If ![]() is infinite, then
is infinite, then
![]() where
where
![]() .
Let
.
Let
![]() be a bijection and let
be a bijection and let
![]() be the
induced bijection given by
be the
induced bijection given by
![]() .
.
Define a function
![]() by
by
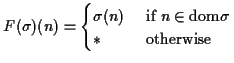
Then ![]() is injective as if
is injective as if
![]() we see that
we see that
![]() and that we have
and that we have
![]() .
.
Composing ![]() with
with ![]() , we see that
, we see that
![]() .
.
![]()
6 (page 165, # 32) Let
![]() be the collection of all finite subsets of
be the collection of all finite subsets of ![]() . Show that if
. Show that if ![]() is
infinite, then
is
infinite, then
![]() .
.
Thus, by problem 26 of page 161, we have that
![]() . However, as
. However, as
![]() , we certainly have
, we certainly have
![]() .
Therefore,
.
Therefore,
![]() .
.
Now, define a function
![]() by
by
![]() .
By definition of a finite set, this function is surjective. Thus,
.
By definition of a finite set, this function is surjective. Thus,
![]() . Again, as every singleton in
. Again, as every singleton in ![]() is a finite set, we
have
is a finite set, we
have
![]() . Therefore,
. Therefore,
![]() .
.
![]()
7 (page 165, # 35) Find a collection
![]() of
of
![]() sets of natural numbers such that any two
distinct members of
sets of natural numbers such that any two
distinct members of
![]() have finite intersection.
have finite intersection.
Claim: Let ![]() be any infinite set with
be any infinite set with
![]() . Let
. Let
![]() .
Then
.
Then
![]() .
.
Proof of claim: We may write
![]() as the disjoint union of
as the disjoint union of
![]() and
and
![]() . By the result of the
previous problem, we have
. By the result of the
previous problem, we have
![]() . Letting
. Letting
![]() ,
We compute
,
We compute
By Euclid's theorem, the set ![]() of prime numbers is a countably infinite set. Hence, the set
of prime numbers is a countably infinite set. Hence, the set
![]() of infinite sets of primes has cardinality
of infinite sets of primes has cardinality
![]() .
.
For each
![]() define
define
![]() .
This association defined a function
.
This association defined a function
![]() . Let
. Let
![]() .
.
Note that for any
![]() the set
the set ![]() is infinite as
is infinite as ![]() is infinite so that there are elements of
is infinite so that there are elements of ![]() with arbitrarily many prime divisors.
with arbitrarily many prime divisors.
If ![]() are two distinct elements of
are two distinct elements of
![]() , then there is some prime which belongs to one set but not the
other. Without loss of generality, we may assume
, then there is some prime which belongs to one set but not the
other. Without loss of generality, we may assume
![]() . Let
. Let
![]() and
and
![]() . Note that if
. Note that if ![]() , then
, then ![]() does not divide
does not divide ![]() while
while ![]() divides every
element of
divides every
element of ![]() . Thus,
. Thus,
![]() is contained in
is contained in
![]() which
is a finite set. Hence,
which
is a finite set. Hence,
![]() is finite. As
is finite. As ![]() is infinite, this implies in particular that
is infinite, this implies in particular that
![]() . Thus, the map
. Thus, the map
![]() is a bijection so that
is a bijection so that
![]() has cardinality
has cardinality
![]() and is almost
disjoint.
and is almost
disjoint.
![]()
8 Show that for any infinite cardinal ![]() , we have
, we have
![]() .
.
As every permutation is a function from ![]() to
to ![]() (and in particular a relation with field
(and in particular a relation with field ![]() ), we have
), we have
![]() so that
so that
![]() .
.
For the other inequality, define a function
![]() by
by
![]() .
Let
.
Let
![]() . To compute the cardinality of
. To compute the cardinality of ![]() we need a claim.
we need a claim.
Claim: Let ![]() be any set with
be any set with
![]() . Then there is a permutation
. Then there is a permutation
![]() having no
fixed points.
having no
fixed points.
Proof of claim: If ![]() is finite, then
is finite, then
![]() for some
for some
![]() with
with ![]() . Let
. Let ![]() be a bijection.
Define
be a bijection.
Define
![]() by
by
![]() if
if ![]() and
and
![]() . Define
. Define
![]() by
by
![]() .
.
If ![]() is infinite of cardinality
is infinite of cardinality ![]() , then as
, then as
![]() , we can find a bijection
, we can find a bijection
![]() . Define
. Define
![]() by
by
![]() .
Let
.
Let
![]() .
.
![]()
From the claim it follows that
![]() .
For if
.
For if ![]() , then
, then
![]() and if
and if
![]() has more than one element,
then we can find (by the claim) a permutation
has more than one element,
then we can find (by the claim) a permutation
![]() having no fixed points so that if
having no fixed points so that if
![]() we have
we have
![]() . Finally, if
. Finally, if
![]() is a singleton, then
is a singleton, then ![]() cannot be in the image of
cannot be in the image of ![]() as any permutation which fixes
as any permutation which fixes ![]() must fix
its complement setwise, and in the case of a singleton, being fixed setwise is the same as being fixed
pointwise.
must fix
its complement setwise, and in the case of a singleton, being fixed setwise is the same as being fixed
pointwise.
There is an obvious bijection between ![]() and the set of subsets of
and the set of subsets of ![]() whose complements are singletons
given by
whose complements are singletons
given by
![]() . Hence,
. Hence,
![]() . As in the proof
the claim in problem 7, we conclude that
. As in the proof
the claim in problem 7, we conclude that
![]() . As
. As
![]() is surjective, we conclude that
is surjective, we conclude that
![]() .
.
Combining this with the other inequality, we conclude that
![]() .
.
![]()