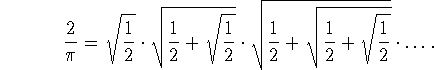
---

Life | Work | Viete's construction of the regular heptagon | Bibliography | Back to the front page

Work
Robin Hartshorne

His first published work, the Canon mathematicus [Canon, 1579] has trigonometric tables computed to 9 decimal places, and contains a systematic collection of trigonometric formulas. Because of many misprints and a misunderstanding with the editor, this volume was not included in his collected works.

Vieta's most significant contributions were in algebra. While letters had been used to describe an unknown quantity by earlier writers, Vieta was the first to also use letters for the parameters or constant coefficients in an equation. Thus, while Cardano solved particular cubic equations such as

Vieta could treat the general cubic equation

where p and q are constants.

Vieta's algebra was significantly more systematic in the formal manipulation of equations than that of his predecessors, but it still does not reach the facility of modern techniques, because he did not consider negative numbers, and did not yet have a symbol for equality. For example, he writes the above cubic equation [Opera, p.86].

A cubus quad. in A, æquetur B quad. in Z.

He used vowels, such as A here, to represent unknowns, and consonants, such as B ,Z, to denote constants. Vieta also preserved the old distinction between linear, planar, and solid quantities, so that represented the solid cube whose side is A. In equations, solids can only be compared with other solids, so what we call p,q he had to call and to preserve homogeneity.

In geometry Vieta gave a solution of the problem of Apollonius referred to above, and also made a study of ``solid" problems such as the trisection of the angle and the construction of the regular heptagon, which use a marked ruler in addition to the Euclidean tools of ruler and compass.

Vieta calculated the value of to ten decimal places, using the method of Archimedes, and also gave an infinite product formula for , one of the earliest occurrences of an infinite product [Opera p. 400]: