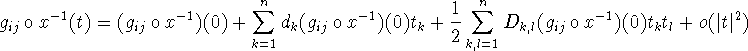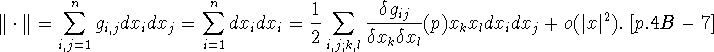
| Life | Work | Mathematics | Bibliography | Back to the front page Mathematics Milena Hering I will start with some definitions and then present the first half of chapter II.2. in ``Über die Hypothesen, welche der geometrie zugrundeliegen". Riemann's defines the notion of a manifold inductively as follows: In a concept whose instances form a continuous manifold, if one passes from one instance to another in a well-determined way, the instances through which one has passed form a simply extended manifold, whose essential characteristic is, that from any point in it a continuous movement is possible in only two directions, forwards and backwards. If one imagines that this manifold passes to another, completely different one, and once again in a well-determined way, that is, so that every point passes to a well-determined point of tha other, then the instances fom. similarly a double extended manifold. In a similar way, one obtains a triply extended manifold when one imagines that a doubly extended one passes in a well-determined way to a completely different one, and it is easy to see how one can continue this construction. (...) [Riemann I.2]
The modern definition says that a manifold has to be locally isomorphic to
On the manifold, Riemann introduces a metric: ...ds equals the squareroot of an everywhere positive homogenuous function of the second degree in the quantities dx in which the copefficients are continuous functions of the quantities x.
So he introduces a norm by
For this purpose, one constructs the system of shortest lines emanating from a given point; the position of an arbitrary point can be determined by the initial direction of the shortest line in which it lies, and its distance, in this line, from the initial point. It can therefore be expressed by the ratios of the quantities
Riemann fixes a point p on his manifold and looks for the location of
another point. He takes the the tangent vector of the Geodesic, the
shortest line on M between p
and q and then the length of this line between p and q. Therefore he
needs an vector,
In place of the
He there diagonalizes the matrix
If one introduces these quantities, then for infinitely small values of x the square of the line element equals
The main part is dealing with the second part of the Taylor expansion of
the functions he uses to define his norm. The corresponding part in the
norm he says to be equal to
Now I will outline the proof of this theorem in modern mathematics. (I
hope sometime, at the moment i will only outline the modern mathematics
needed to state the statement.)
Therefore we need the Riemannian normal coordinates which he
introduces
in the first part. One chooses an othonormal basis Then one takes the vector on and since where
Spivak then states some Propositions about these terms. 1. In a Riemannian normal coordinate system x at p we have
2. Then
3. Let Q be a quadratic function of 2n variables, where Then
for all
4. A quadratic function with (1) of 3. satisfies the two equivalent consitions of 3. if and only if it can be written as
5. In a Riemannian normal coordinate system x at p, the numbers satisfy
Therefore by 4. it can be written in the way Riemann asserts and one can
define a number Q(W) for any 2-dimensional subspace with
The theorem can then be stated like this:
If M is 2-dimensional and
(Since Spivak
divides by the square of the parallelogram instead of the area of the
triangle spanned by the vectors like Riemann, he does not need the factor
|
and it is quite likely that Riemann already was aware of this
property of manifolds. [Spivak, 4B-2]
, where
. The inner product from which is comes is called the
Riemannian metric on a manifold M and a manifold with a Riemannian
metric is a Riemannian Manifold. From now on every manifold will be
Riemannian.
, i.e., the quantities
dx
at the origin of this shortest line and by the length s of this line.
formed from them in such a way that the initial value of the square of the
line element will be equal to the sum of the squares of these expressions,
so that the independent variables are: the quantity s and the ratios of
the quantities 
proportional to them, but such that the sum
of their squares equals 
. 
with 
and
gets a diagonal matrix 
. Finally he takes 
,
such
that 
and denotes 
by 
.
, but the next order
term in its expansion equals a homogenous expression of the second degree
in the 
quantities 
and is consequently an infinitely small quantity of the fourth
order, so that one obtains a finite quantity if one divides it by the
square of the infinitely small triangle at whose vertices the variables
have the values 
.
This quantity remains the same as long as the quantities x and dx are
contained in the same binary linear forms, or as long as the two shortest
lines from the initial point to x and from the initial point to dx
remain in the same surface element, and therefore depends only on the
position and direction of that element. It obviously becomes zero if the
manifold in question is flat, i.e., if the square of the line element is
reducible to 
it becomes equal to the quantity which Privy
Councillor Gauss has called the curvature of a surface.
[Riemann, 4A-11/12]
. Then he defines a quantity
by dividing this sum by the square of the triangle spanned by 
and 
. He states, that this quantity is not
influenced by a linear transformation of the vectors. Because if
, there is no second term in the Taylor expansion, this
quantity is zero in this case. This is the only ``Proof" he gives that
this quantity has to be equal to 
,
where
R is a subset of M and 
.[Spivak, p. 3A-4]
in the
tangent space 
of the fixed point p. Then a coordinate system is
defined by 
, we have
,
we get 
matrices A if and only if: 
by
any basis for W.
[p.4B-24]
, then 
.)