| The Abstractor
| Elementary Notions
| A Fourth Dimension
| A Division Algebra
| Closure
| An Example of Hamilton's Work
| Bibliography
| Back to the front page
A Division Algebra
Joseph Johnson
Hamilton had discovered what modern mathematicians term a skew field. That is, the system satisfies the following
axioms applied to the direct sum of four real additive groups, under Hamilton's definitions of equality, addition, and
multiplication. Let 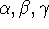 be any quaternions with be any quaternions with 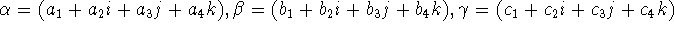
(1) Closure of (a) addition and (b) multiplication. Both the addition and multiplication of two quaternions yields another
quaternion.
(2) Commutativity of (a) addition and falsity of (b) multiplication commutativity. It is easy to see that
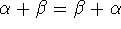 . Of course . Of course 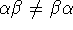 in general. in general.
(3) Associativity of (a) addition and (b) multiplication. Clearly 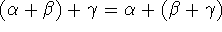 , by
properties of real numbers. The proof of multiplication associativity has been described as ``torture" by at least one
mathematician. , by
properties of real numbers. The proof of multiplication associativity has been described as ``torture" by at least one
mathematician.
(4) (a) Addititive and (b) multiplicative identities. The addititve identity is simply 0.
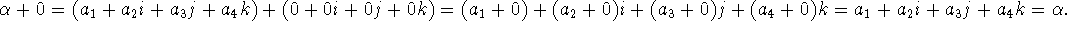
The mulitiplicative identity is 1=(1+0i+0j+0k).
(5) (a) Additive and (b) multiplicative inverses. The additive inverse of 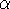 is simply is simply
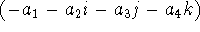 . Finding the multiplicative inverse of . Finding the multiplicative inverse of 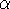 is more detailed. The use of the
aforementioned modulus function, is more detailed. The use of the
aforementioned modulus function,  , is crucial. , is crucial.
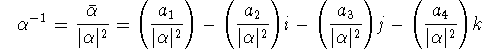
where 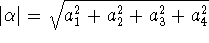 . This can be derived as a
consequence of conjugacy in Quaternions (see Elements Paragraph 187). Every quaternion . This can be derived as a
consequence of conjugacy in Quaternions (see Elements Paragraph 187). Every quaternion 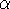 has a conjugate has a conjugate
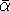 such that such that 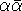 is a real number. This allows us to set is a real number. This allows us to set 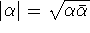 .
The explicit conjugate of .
The explicit conjugate of 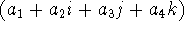 is is 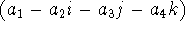 (which is
analogous to conjugacy of complex numbers). (which is
analogous to conjugacy of complex numbers).
(6) Distributive laws. It seems almost amazing that the Quaternions are in fact distributive. That is
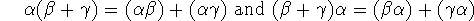
If this axiom did not hold, the Quaternions would be utterly uninteresting. It would represent two separate group structures
(after deleting 0 in the multiplicative case) - hardly impressive to most mathematicians.
| The Abstractor
| Elementary Notions
| A Fourth Dimension
| A Division Algebra
| Closure
| An Example of Hamilton's Work
| Bibliography
| Back to the front page
|