Mathematics 115
Fall, 2000
3 Evans Hall, MWF 11:10-12

Professor Ken Ribet

885 Evans Hall

Regular office hours Tu 11-noon, Th 12-1, Fri 2-3
Office telephone: 642 0648
Fax number: 642 8204
Secretary: 642 5026

Exam week office hours:

• Monday, December 11 -- 2-3:30PM
• Tuesday, December 12 -- 11:30AM-12:30PM

Textbook

When you discover misprints in the textbook, please e-mail me with what you've found. I'm compiling a list, which I'll send to the author at the end of the semester.

Syllabus

It looks as if I will follow the book's table of contents, treating Chapters 1 and 2 pretty superficially. We should certainly be able to cover Chapter 8, which treats cryptology. By the end of the course, we should have covered the very important Chapter 11. If there's time, we'll talk about continued fractions as well (Chapter 12).

Examinations

• First Midterm: Friday, September 29 (questions and answers). Here's how the scores were distributed:

  
  
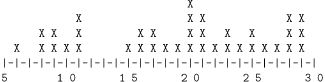  Median = 20
  Average = 19.2
  Maximum possible score = 30
  

• Second Midterm, Friday, November 3 (questions and answers). Here's how the scores were distributed:

  
  
  Median = 18
  Average = 18.6
  Maximum possible score = 30
  

• Final Exam, Wednesday December 13, 12:30-3:30 (exam group #2), 141 McCone Hall (questions and answers). Here's how the scores were distributed:

  
  
  Median = 30
  Average = 29.7
  Maximum possible score = 50
  

If you'd like to see some questions that I've given in exams for this course before, you can look at the Spring, 1998 and the Fall, 1999 questions. The first of these courses was taught in 50-minute MWF courses, while the second was taught in 80-minute TuTh courses. These documents, by the way, are in Adobe Acrobat format.

Homework

For numerical problems, the grader encourages you to use computer software as you see fit. Be sure, however, to include printouts that explain what you did.

Your homework score for the class is computed in such a way that your lowest score is ignored and your next lowest score is given only half its usual weight. There will be 14 assignments, each worth 20 points. Thus the maximum possible homework score will be 250.

1. Assignment due September 6:
   • § 1.4: 5cd, 6, 8, 14, 17, 30, 36
   • § 3.1: 5, 7, 10, 16, 25
2. Assignment due September 11:
   • § 3.2: 9, 15, 16, 25
   • § 3.3: 1a, 3a, 5c, 7c, 9
   • § 3.4: 3, 7
3. Assignment due September 18:
   • Write the product (x-a)(x-b)(x-c)...(x-z) a simply as possible.
   • Check out the schedule for the MSRI Chern conference that begins on September 14. The talks on September 16 are intended for a very wide audience. By the way, you might be interested in other MSRI activities this semester. See for example the number theoretic cryptographgy workshop and the associated short course on complexity.
   • § 3.4: 10, 14, 15, 17, 18
   • § 3.5: 3ac, 4a
   • § 3.6: 2ace
   • § 4.1: 3, 6def, 7, 16, 28
4. Assignment due September 25:
   • § 4.2: 2ab, 4 (assume that m is prime!), 6, 8d, 12, 16
   • § 4.3: 4c, 8, 22
   • § 4.4: 2abc, 9, 10
5. Assignment due October 4:
   • § 4.5: 2ab, 7, 8bc
   • § 4.6: 1f
   • § 5.1: 4, 12, 22
6. Assignment due October 11
   • § 6.1: 4, 6, 10, 12, 14, 16, 26, 28
   • § 6.2: 6
   • Browse the companion website for our textbook. It has just been put on line.
   • Look at the Prime Pages, which are maintained by Chris Caldwell, a number theorist who got his doctorate from Berkeley. The Mersenne prime page mentions the conjecture that there are infinitely many Mersenne primes and infinitely many composite numbers of the form 2^p-1 with p prime.
7. Long and hard assignment due October 16:
   • § 6.3: 2, 6, 10, 18
   • § 7.1: 6, 10, 14, 22
   • § 7.2: 2def, 4, 10, 12
   • § 7.3: 4ac, 6, 10, 16
8. Assignment due October 23:
   (Note that the number-theoretic cryptography workshop begins at the MSRI on October 16.)
   • § 7.4: 11, 12, 23, 24
   • § 9.1: 2cd, 4def, 10, 12, 18
   • § 9.2: 2cd, 6, 8, 11, 12, 16 (for this one, take p>5)
   Our grader, John Voight, will be lecturing on perfect numbers in class on Friday, October 27.
9. Assignment due October 30:
   
   • § 9.3: 6ad, 8ad, 10, 14, 15, 16
   • § 9.4: 2ab, 4, 8, 9, 10
10. Assignment due November 8:
    
    • § 9.5: 2, 4, 5, 8
    • § 8.1: 4, 6, 8, 10
    • § 8.2: 2, 8, 10ab
11. Assignment due November 15:
    
    • § 8.4: 2, 6
    • § 11.1: 5, 6, 7, 10, 12, 14, 27
    • § 11.2: 4, 6
    Note that office hours on November 16 will be 2-3PM instead of 12-1PM.
12. Assignment due November 22:
    
    • § 11.2: 10, 11, 12 [Note that much of #12 will be done in class on November 15.]
    • § 11.3: 1cd, 5, 6
    • Suppose that p is an odd prime and that p is the sum of a-squared and b-squared. If a is odd, show that a is a square modulo p. Example: the prime 977 is the sum of the squares of 31 and 4; we may conclude that 31 is a square modulo 977.
13. Assignment due December 1:
    
    • § 11.4: 2, 3, 4, 5, 6
14. Assignment due December 8:
    
    • § 12.1: 9f, 13
    • § 12.2: 2ef, 4ae, 8
    • § 12.3: 1ac, 2ab, 5
    • § 12.4: 6ac

Grading

Miscellaneous links related to number theory and/or this course

• Fermat's Last Tango
• Maths Posters in the London Underground
• A newly discovered prime number (October 21, 2000)
• TeachMath at Berkeley
• Least primitive root of prime numbers
• Teach for America (February 13, 1998)
• Large prime discovered by 19-year-old sophomore (February 3, 1998)
• Fermat's Last Theorem T-shirt (we will put in a group order if there's interest)
• Number Theory Web
• Life by the Numbers

Kenneth A. Ribet , Math Department 3840, Berkeley CA 94720-3840

This page last modified