Math 290: PDE Learning Seminar (Fall 2023)
Non-linear wave equations at critical regularity
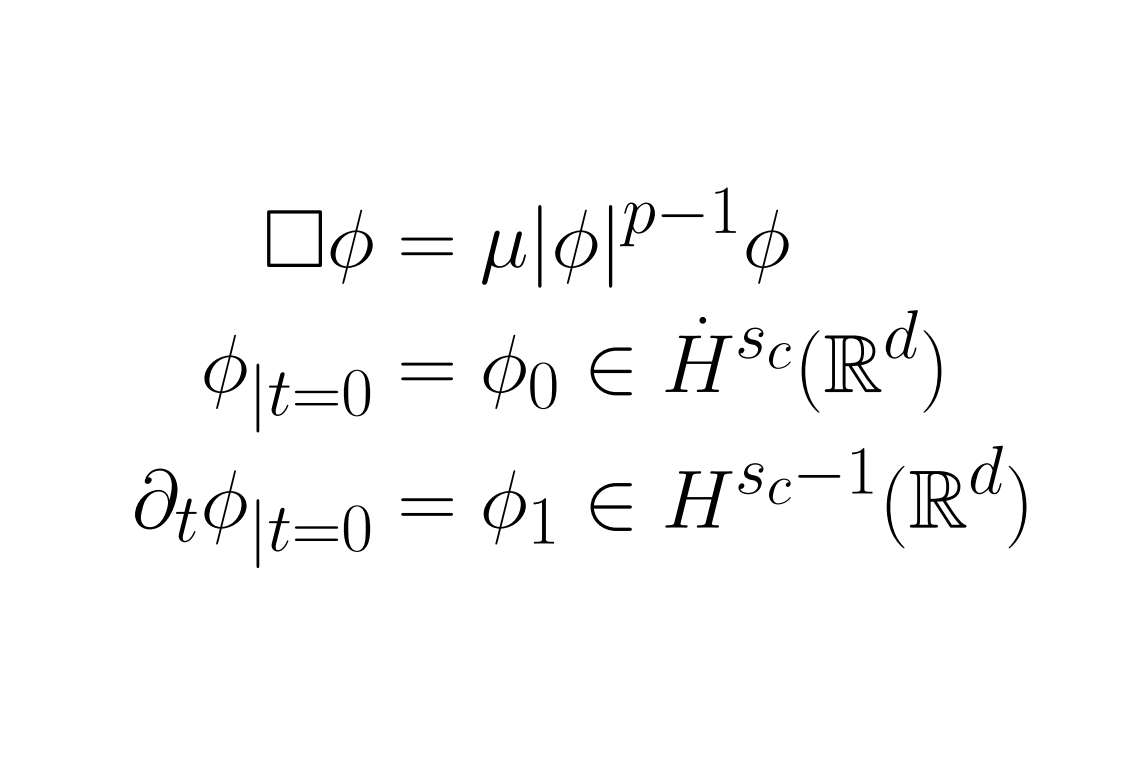
Abstract
This learning seminar will study geometric wave equations, namely the semi-linear wave equation, \(\Box \phi = \mu |\phi|^{p - 1} \phi\), and the wave maps equation, \(\Box \phi^i = -\mathcal S^i_{jk} (\phi) \partial_\alpha \phi^j \partial^\alpha \phi^k\), at critical regularity. Our main goal will be to cover the following two topics:- the proof of the threshold theorem for energy critical wave maps à la Sterbenz-Tataru, and
- the recent proof of soliton resolution for energy critical wave maps in equivariant symmetry by Jendrej-Lawrie.
Coordinates
The seminar meets on Fridays at 2:15 PM to 4:00 PM in Evans 891. If you would like to join the mailing list, please click here. Notes for each talk will be posted to the following Google Drive folder.
Schedule (click title to show/hide abstract)
| Date | Topic | Ref. | Speaker |
| 9/15 |
Bubbling argument for energy-critical equivariant wave maps and defocusing NLW
Abstract: A basic strategy for proving large data global regularity and scattering for critical equations is bubbling, i.e. extraction of a nontrivial stationary solution via blow-up analysis. I will discuss two instances of this argument, in the context of equivariant wave maps and defocusing NLW. |
[1, 8] | Sung-Jin |
| 9/22 |
Threshold theorem for focusing NLW
Abstract: We study the Threshold Theorem of Kenig and Merle (2006) for focusing energy critical NLW. The theorem allows us to determine global scattering versus finite time blow up by comparing candidate initial data against the special ground state solution \(W\). The formal statement is for \((u_0, u_1) \in \dot H^1 \times L^2\) with \(E(u_0,u_1) < E(W)\) (where \(E\) is the conserved energy for the system). If \(||u_0||_{\dot H^1} < ||W||_{\dot H^1}\) then the solution is global and scatters, but if \(||u_0||_{\dot H^1} >||W||_{\dot H^1}\) then the solution blows up in finite time. The proof of the finite time blow up is the standard argument of Glassy; the proof of the global scattering is much more involved, using the so called "concentration compactness/rigidity method" in a huge proof by contradiction which involves extracting a profile \(u^*\) from a sequence of pathological initial data whose momentum ultimately contradicts itself. |
[3] | Ryan |
| 9/29 |
Global regularity and scattering of wave maps in \(d\geq 4\) with small critical Sobolev data
Abstract: Shatah-Struwe [4] proved the global wellposedness for scaling critical wave maps equations when \(n \geq 4\) under mild topological assumptions. Their proof relies on the existence of Coloumb gauge [13, Uhlenbeck '84]. I will mainly discuss the Shatah-Struwe global wellposedness result and briefly compare it with Tao's [7] paradifferential calculus approach. |
[4] | Ning |
| 10/6 |
Scattering threshold for the focusing nonlinear Klein-Gordon equation
Abstract: I will talk about the paper by Ibrahim-Masmoudi-Nakanishi, which shows the scattering/blow-up dichotomy for the focusing nonlinear Klein-Gordon equation. The method is similar to that of Kenig-Merle, i.e. application of concentration compactness. |
[5] | Zhongkai |
| 10/13 |
Global well-posedness of wave maps in low dimensions at critical regularity
Abstract: I am going to talk about the main result from a paper by Tataru, in which he shows that the wave maps equation is globally well-posed for small initial data at critical Sobolev regularity in low dimensions (\(d = 2, 3, 4\)). The proof relies on some spaces that were essentially defined by Tao in his earlier paper, in which he obtained a global regularity result for solutions to the wave maps equation with small initial data in the critical Sobolev norm. I am going to try to motivate the construction of the aforementioned spaces, while discussing some ideas from the proof of one of the key results in Tataru's paper. |
[6, 7] | Ovidiu |
| 10/20 |
Large data regularity theory for energy critical wave maps
Abstract: We present the energy dispersion method of Sterbenz and Tataru, which provides a constructive alternative to the concentration compactness method of Kenig and Merle. Combined with the bubbling argument, this completes the large data regularity theory for energy-critical wave maps. |
[8, 9] | Jason & Sung-Jin |
| 10/27 |
Codimension \(1\) stability of the ground state for the radial focusing NLW
Abstract: I will discuss aspects of the paper "On the focusing critical semi-linear wave equation" by Krieger and Schlag. |
[10] | Ely |
| 11/3 |
Asymptotic decomposition for semilinear wave and equivariant wave map equations
Abstract: I will talk about the soliton resolution conjecture along a sequence of times for the equivariant wave map equations in the case of finite time blowup, following a paper by H. Jia and C. Kenig. |
[11] | Xiaoyu |
| 11/10 | Academic holiday | ||
| 11/17 |
Soliton resolution for equivariant wave maps
Abstract: We will talk about the paper of Jacek Jendrej and Andrew Lawrie on soliton resolution for 2D equivariant wave maps. |
[12] | Yuchen & Sung-Jin |
| 11/24 | Thanksgiving |