This post is a toy investigation of the cluster move as a transformation of skeleta.  It contains any new ideas.

The cluster move should represent the relationship between opposite ends of a continuous process labeled by a one-parameter family of Morse functions whose skeleta transform by a blow-down, blow-up procedure.  Arborealization is realized by the blow-up, so a singular Lagrangian skeleton should sit at the midpoint of this process.

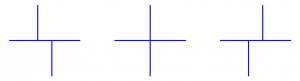
As David T. has explained, the baby example of such a transformation should be the BGP moves, realized as equivalences of microloclal categories.  These moves are described by local processes. Here’s the familiar picture.

 

But skeleta are not local objects, so here is a global example which models the same transformation. Take $X$ to be an elliptic curve minus a point. Note that in the pictures above we can identify the sides as for a torus, so then if the left and right diagrams are skeleta they are obtained by attaching a Weinstein one-cell with boundary a zero-sphere in different orientations.

We model the torus this as $\mathbb C/\Lambda,$ where $\Lambda$ is generated by translations by $1$ and $\tau.$ Let $\mathfrak{p}$ = $\mathfrak p_\tau(z)$ be the Weierstrass $\mathfrak p$-function. Define a proper, subharmonic function on $X$ by $f = |\mathfrak p|^2.$  (We remove the point $z=0$ at which $\mathfrak p$ has a double pole.) Then $d f = \overline{\mathfrak p}\mathfrak{p}’ dz$ plus complex conjugate, and has zeros when $\mathfrak{p}$ or $\mathfrak{p}’$ vanish.

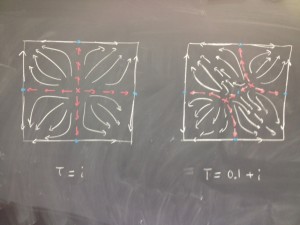
Now recall $(x,y) = (\mathfrak{p}(z),\mathfrak{p}'(z))$ embeds $X$ as a Weierstrass cubic $y^2 = 4x^3 …$, and therefore $y=0$ has three solutions while $x= 0$ has two. (The reason that there are different numbers of intersection points with divisors is that the compactification naturally lives in $\mathbb P^2_{1,2,3}$, not ordinary $\mathbb P^2$.) We claim that the solutions with $x= \mathfrak = 0$ are minima while the saddle points have $y=0.$ (In general recall, the $k$-cells of the skeleton are Morse index $k$ critical points.  Note here that the Euler characteristic is $-1$ as appropriate for $X$ since its a torus minus a point.) To see this, near a zero of $\mathfrak p$, after a linear change of coordinates we have $\mathfrak p \sim u$, so $f \sim |u|^2$ and we have a minimum.  On the other hand, near a zero of $\mathfrak p’$ we have $\mathfrak p \sim a + \frac{1}{2}u^2$ and $f \sim |a|^2 + Re(\overline{a}u^2).$  Up to constants this is $a_1 (u_1^2 – u_2^2) – a_2 u_1 u_2$, so $\det {\rm Hess}(f) \sim -|a|^2$ is negative and we have a saddle point.  At the nongeneric point $\tau = i,$ there is only one minimum and two saddles. This produces the $+$ sign skeleton. Note the four upward gradient flows are related the complex multiplication.

Here is a picture of what the flow lines look for $\tau = i$ and for the nearby Morse function with $\tau = 0.1 + i.$ The pictures were made from computer calculations which used the (incomplete) Euclidean metric, but I think the qualitative behavior
should be accurate.

 

Anyhoo, it would be nice to have a similar model in four dimensions.  A natural four-manifold to consider — analogous to what we just did — would be the resolution of the $A_2$ singularity with its skeleton of two $S^2$’s glued at a point. This should be the non-generic configuration with one minimum and two index-two points. The $A_2$ resolution is a toric variety and has a map to $\mathbb C$ that we can use to produce a proper Morse function.  Alternatively, we can use a hyperkahler rotated version as $y^2 + z^2 = p(x)$, where $p$ is a cubic polynomial.  I haven’t been able to make choices and derive skeleta yet, though.