- Splitting mass points using
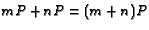 is useful when dealing
with transversals. In
is useful when dealing
with transversals. In
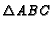 , let
, let  be in
be in 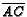 such that
such that 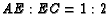 , let
, let
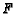 be in
be in 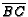 such that
such that 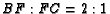 , and let
, and let 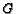 be in
be in
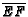 such that
such that 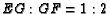 .
Finally, let ray
.
Finally, let ray 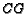 intersect
intersect 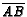 in
in 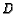 . Find
. Find 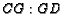 and
and
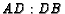 .
.
Solution: Draw the figure! Assign weight 2 to 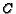 and weight 1 to
and weight 1 to 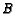 so
that
so
that 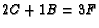 . It is now necessary to
have weight 6 at
. It is now necessary to
have weight 6 at  to ``balance"
to ``balance" 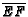 . Since
. Since 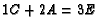 , we
have
, we
have 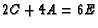 ,
so assign another
weight 2 to
,
so assign another
weight 2 to 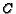 for a total weight of 4 at
for a total weight of 4 at 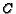 and assign a weight of 4 to
and assign a weight of 4 to
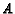 . Then
. Then 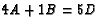 .
Now the ratios can be read directly from the figure.
.
Now the ratios can be read directly from the figure. 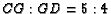 and
and
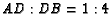 .
.
- In the previous problem,
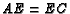 ,
, 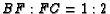 , and
, and 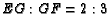 . Show that
. Show that
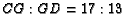 and
and 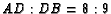 .
.
- In the previous problem, let
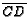 be a median, let
be a median, let
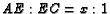 and
and 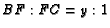 . Show
that
. Show
that 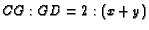 and
and
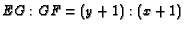 .
.
- For an altitude, say
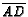 in
in
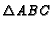 , note
that
, note
that
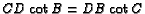 . Therefore, assign weights proportional to
. Therefore, assign weights proportional to 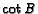 and
and
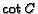 to
to 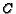 and
and 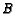 , respectively. Let
, respectively. Let
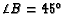 ,
,
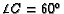 ,
and let the angle bisector of
,
and let the angle bisector of 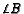 intersect
intersect 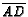 in
in  and
and 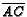 in
in 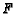 .
Show that
.
Show that
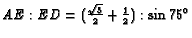 and
and
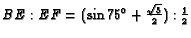 .
.
- In the previous problem, change
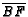 from angle
bisector to median. Show that
from angle
bisector to median. Show that
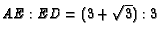 and
and
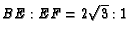 .
.
- Prove that the altitudes of an acute triangle are concurrent using
mass points. Review the
clever method of showing this by forming a triangle for which the given
triangle is the medial
triangle and noticing that the perpendicular bisectors of the large
triangle contain the altitudes
of the medial triangle.
- Let
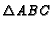 be a right triangle with a
be a right triangle with a 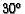 angle
at
angle
at 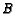 and a
and a 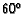 angle at
angle at 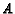 . Let
. Let 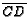 be the altitude to the hypotenuse and let
the angle bisector at
be the altitude to the hypotenuse and let
the angle bisector at
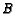 intersect
intersect 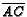 at F and
at F and 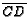 at
at  . Show that
. Show that
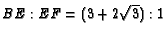 and
and
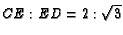 .
.
- Let
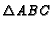 be a right triangle with
be a right triangle with 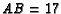 ,
, 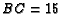 ,
and
,
and 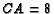 .
Let
.
Let 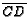 be the altitude to the hypotenuse and let the angle
bisector at
be the altitude to the hypotenuse and let the angle
bisector at
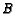 intersect
intersect 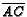 at F and
at F and 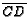 at
at  . Show that
. Show that
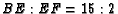 and
and 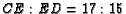 .
.
- Generalize the previous problems. Let
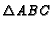 be a right
triangle with
be a right
triangle with 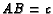 ,
,
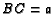 , and
, and 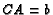 . Let
. Let 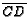 be the altitude to the hypotenuse
and let the angle bisector
at
be the altitude to the hypotenuse
and let the angle bisector
at 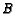 intersect
intersect 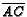 at F and
at F and 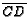 at
at  . Show
that
. Show
that
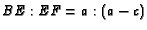 and
and 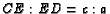 .
.
- Prove Ceva's Theorem for cevians that intersect in the interior of
the triangle.
Three cevians of a triangle are concurrent if and only if the
products of the lengths of the
non-adjacent sides are equal. (Hint: In
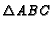 , let
, let  ,
,
 ,
, 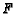 be the intersection
points of the cevians in sides
be the intersection
points of the cevians in sides 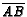 ,
, 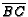 and
and
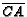 , respectively.
Let
, respectively.
Let 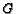 be the intersection of the cevians,
be the intersection of the cevians, 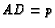 ,
, 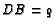 ,
, 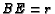 , and
, and
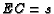 . Assign weight
. Assign weight
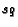 to
to 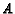 ,
, 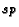 to
to 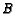 , and
, and 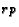 to
to 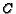 ).
).
- Prove Menelaus' Theorem. If a transversal is drawn across three
sides of a triangle
(extended if necessary), the product of the non-adjacent lengths are equal.