- If
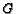 is on
is on 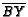 then
then 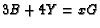 . What is
. What is 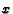 ? What
is
? What
is 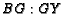 ?
?
- If
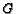 is on
is on 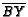 then
then 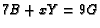 . What is
. What is 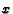 ? What
is
? What
is 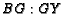 ?
?
- In
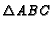 ,
, 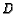 is the midpoint of
is the midpoint of 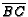 and
and
 is the
trisection point of
is the
trisection point of 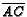 nearer
nearer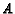 . Let
. Let 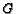 =
=
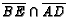 .
Find
.
Find 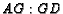 and
and 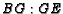 .
.
Solution: Draw the figure! Assign weight 2 to 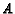 and weight 1 to each of
and weight 1 to each of
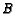 and
and 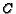 .
Then
.
Then 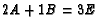 and
and 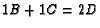 .
Note that the center of mass of the system is
.
Note that the center of mass of the system is
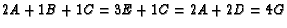 . From this
we can see that
. From this
we can see that
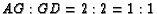 and
and 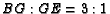 .
.
- ( East Bay Mathletes April 1999) In
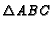 ,
, 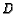 is
on
is
on 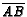 and
and  is the
on
is the
on 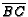 . Let
. Let 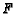 =
=
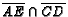 .
. 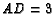 ,
,
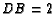 ,
, 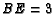 and
and 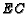 =4
Find
=4
Find 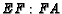 in lowest terms.
in lowest terms.
- Show that the medians of a triangle are concurrent and the point of
concurrency
divides each median in a ratio of 2:1. (Hint: Assign a weight of 1 to each
vertex.) How does this
show that the six regions all have the same area?
- ( Varignon's Theorem (1654-1722)) If the midpoints of
consecutive sides of a quadrilateral
are connected, the resulting quadrilateral is a parallelogram. (Hint:
Assign weight 1 to each vertex
of the original quadrilateral.)
- In quadrilateral
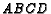 ,
,  ,
, 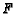 ,
, 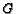 , and
, and 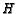 are the trisection
points of
are the trisection
points of 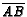 ,
,
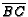 ,
,
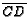 , and
, and 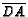 nearer
nearer 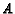 ,
, 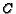 ,
, 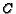 ,
, 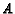 ,
respectively. Let
,
respectively. Let
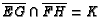 . Show that
. Show that 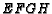 is a parallelogram.
is a parallelogram.
- Generalize the previous problems for
 ,
, 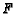 ,
, 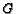 , and
, and 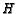 divide
the sides in a
ratio of
divide
the sides in a
ratio of 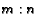 .
.