- ( AHSME 1964 #35) The sides of a triangle are of lengths 13, 14,
and 15. The altitudes of
the triangle meet at point
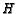 . If
. If 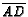 is the altitude to the
side of length 14, what is the ratio
is the altitude to the
side of length 14, what is the ratio
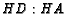 ?
?
- ( AHSME 1965 #37) Point
 is selected on side
is selected on side 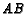 of triangle
of triangle
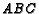 in such a way that
in such a way that
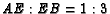 and point
and point 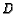 is selected on side
is selected on side 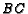 so that
so that 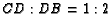 .
The point of intersection
of
.
The point of intersection
of 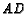 and
and 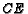 is
is 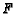 . Find
. Find
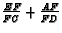 .
.
- ( AHSME 1975 #28) In triangle
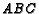 ,
, 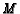 is the midpoint of side
is the midpoint of side
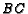 ,
, 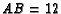 and
and 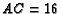 .
Points
.
Points  and
and 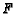 are taken on
are taken on 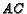 and
and 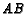 , respectively, and lines
, respectively, and lines 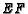 and
and 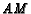 intersect at
intersect at 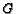 .
If
.
If 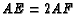 then find
then find 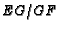 .
.
- ( AHSME 1980 #21) In triangle
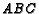 ,
,
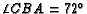 ,
,  is the midpoint of side
is the midpoint of side 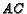 and
and 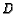 is a point on side
is a point on side 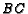 such that
such that 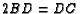 ;
; 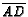 and
and
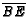 intersect at
intersect at 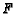 . Find the ratio of the area of triangle
. Find the ratio of the area of triangle 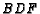 to the area
of quadrilateral
to the area
of quadrilateral 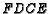 .
.
- ( NYSML S75 #27) In
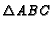 ,
, 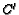 is on
is on
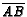 such that
such that
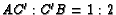 , and
, and 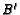 is on
is on 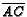 such that
such that
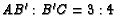 . If
. If
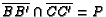 and if
and if
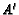 is the intersection
of ray
is the intersection
of ray 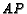 and
and 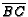 then find
then find  .
.
- ( NYSML F75 #12) In
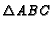 ,
, 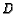 is on
is on
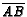 and
and  is on
is on
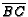 . Let
. Let
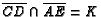 and let ray
and let ray
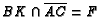 . If
. If 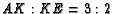 and
and 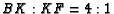 , then find
, then find 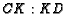 .
.
- ( NYSML F76 #13) In
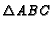 ,
, 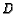 is on
is on
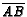 such that
such that
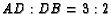 and
and  is on
is on 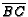 such that
such that 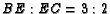 . If ray
. If ray
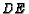 and ray
and ray 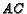 intersect at
intersect at 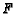 , then find
, then find 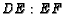 .
.
- ( NYSML S77 #1) In a triangle, segments are drawn from one
vertex to the trisection
points of the opposite side . A median drawn from a second vertex is
divided , by these segments,
in the continued ratio
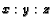 . If
. If 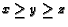 then find
then find 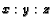 .
.
- ( NYSML S77 #22) A circle is inscribed in a 3-4-5 triangle. A
segment is drawn from the
smaller acute angle to the point of tangency on the opposite side. This
segment is divided in the
ratio
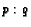 by the segment drawn from the larger acute angle to the point
of tangency on its opposite
side. If
by the segment drawn from the larger acute angle to the point
of tangency on its opposite
side. If 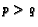 then find
then find 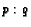 .
.
- ( NYSML S78 #25) In
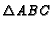 ,
,
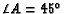 and
and
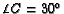 .
If altitude
.
If altitude 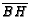 intersects median
intersects median 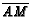 at
at 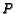 , then
, then
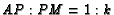 . Find
. Find 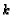 .
.
- ( NYSML F80 #13) In
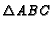 ,
, 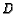 is the midpoint
is the midpoint
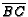 and
and  is the midpoint of
is the midpoint of 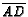 . If ray
. If ray 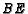 and intersects
and intersects
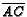 at
at 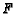 . Find
the value of
. Find
the value of
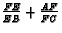 .
.
- ( ARML 1989 T4) In
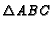 , angle bisectors
, angle bisectors
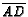 and
and
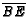 intersect at
intersect at 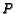 . If
. If 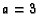 ,
, 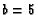 ,
, 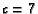 ,
, 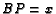 , and
, and 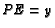 ,
compute the ratio
,
compute the ratio 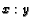 , where
, where 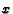 and
and 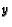 are relatively prime integers.
are relatively prime integers.
- ( ARML 1992 I8) In
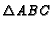 , points
, points 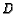 and
and  are
on
are
on 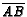 and
and
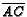 , respectively. The angle bisector of
, respectively. The angle bisector of 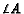 intersects
intersects
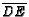 at
at 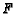 and
and 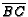 at
at 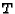 . If
. If
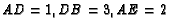 , and
, and 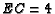 ,
compute the ratio
,
compute the ratio 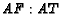
- In the previous problem, if
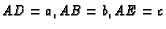 and
and 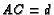 then show
that
then show
that
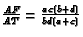 .
.
- ( AIME 1985 #6) In triangle
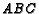 , cevians
, cevians 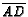 ,
,
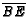 and
and 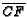 intersect at
point
intersect at
point 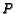 . The areas of triangles
. The areas of triangles 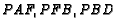 and
and 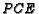 are 40,30,35 and
84, respectively. Find the
area of triangle
are 40,30,35 and
84, respectively. Find the
area of triangle 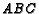 .
.
- ( AIME 1988 #12) Let
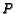 be an interior point of triangle
be an interior point of triangle 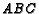 and extend lines from the
vertices through
and extend lines from the
vertices through 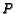 to the opposite sides. Let
to the opposite sides. Let 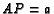 ,
, 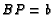 ,
, 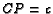 and
the extensions from
and
the extensions from 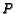 to
the opposite sides all have length
to
the opposite sides all have length 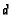 . If
. If 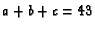 and
and 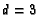 then find
then find
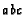 .
.
- ( AIME 1989 #15) Point
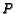 is inside triangle
is inside triangle 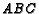 . Line
segments
. Line
segments
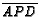 ,
,
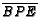 , and
, and
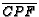 are drawn with
are drawn with 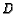 on
on
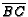 ,
,  on
on 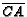 ,
and
,
and 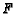 on
on 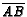 . Given that
. Given that 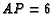 ,
, 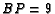 ,
, 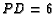 ,
, 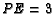 ,
and
,
and 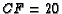 , find the area
of triangle
, find the area
of triangle 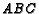 .
.
- ( AIME 1992 #14) In triangle ABC,
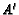 ,
, 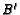 , and
, and
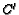 are on sides
are on sides
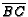 ,
, 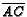 ,
, 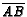 , respectively. Given that
, respectively. Given that
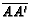 ,
,
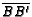 , and
, and
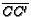 are concurrent at the
point
are concurrent at the
point 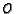 , and that
, and that
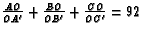 ,
find the value of
,
find the value of
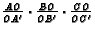 .
.
- (Larson [ 14] problem 8.3.4) In triangle
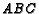 , let
, let 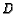 and
and  be the trisection points of
be the trisection points of 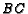 with
with 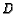 between
between 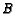 and
and
 . Let
. Let 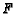 be the midpoint of
be the midpoint of 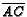 , and let
, and let 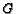 be the
midpoint of
be the
midpoint of
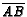 . Let
. Let 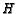 be the intersection of
be the intersection of 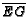 and
and
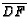 . Find the
ratio
. Find the
ratio 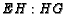 .
.
- Use nonconcurrency problems #4 and #5 to show that the triangle
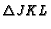 is
one-seventh the area of
is
one-seventh the area of
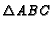 . Generalize the problem using
points which divide the
sides in a ratio of
. Generalize the problem using
points which divide the
sides in a ratio of 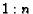 to show the ratio of the areas is
to show the ratio of the areas is
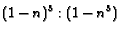 . This can be generalized
even further using different ratios on each side. It is known as Routh's
Theorem. See [ 15]
[ 16] and [ 17].
. This can be generalized
even further using different ratios on each side. It is known as Routh's
Theorem. See [ 15]
[ 16] and [ 17].