Physical Effects/Overview of Mechanism:
Two types of surface diffusion can play important roles in coverage and deposition layers; bulk diffusion, which is the global macro-motion of the material within the deposited layer, and surface diffusion, which relates to the motion of metal boundaries. Here, we examine the effects of surface diffusion on the shape of the deposition layer.
Cale and Jain (Cale, T.S., Jain, M.K., Tracy, C.J., and Duffin, R., submitted for publication, J. Vac. Sci, Tech, B, 1996) have performed carefully fit numerical experiments to match experimental evidence of surface diffusion effects of aluminum-(1.5%)copper films. They propose a model which contains a term which depends on the second derivative of the curvature.
We point out the motion under the second derivative of curvature is reminiscent of the problem of flow under curvature. However, the problem is delicate because this leads to a time-dependent fourth order partial differential equation, and the presence of the fourth derivative requires an exceedingly small time step for stability in an explicit scheme; the linear fourth order heat equation has a stability time step requirement of the form O(dt /h ^4); where dt is the time step and h is the space step. While such schemes can in fact be made implicit to allow a larger time step, the price is considerable more work to evaluate the term.
Level Set Formulation:
The narrow band level set method is particularly well-suited to this sort of problem, due to the embedded representation of the surface. Straightforward finite difference schemes based on central differences may be used to approximate the appropriate higher derivatives.
Results and Sample Simulations:
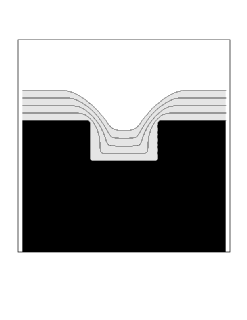
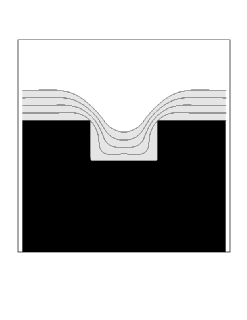
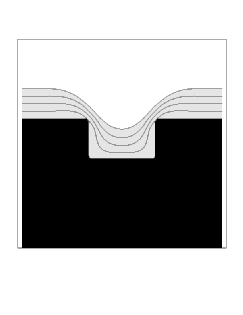
We show two sample simulations. First, we show the case of straightforward isotropic deposition, modified by a surface diffusion term which depends on the second derivative of curvature. More precisely, we use a speed function of the form
where eps is the diffusion coefficient, and K is the local curvature. As the surface diffusion coefficient is increased, the profile is rounded and muted by this effect.
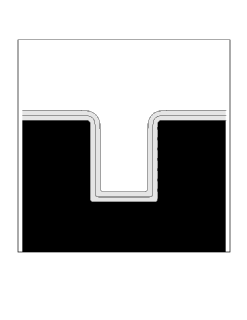
|
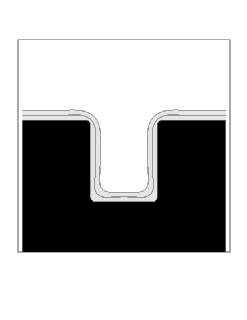
|
| Diffusion Coefficient = 0.0 | Diffusion Coefficient = 0.0025 |
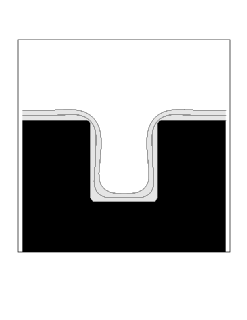
|
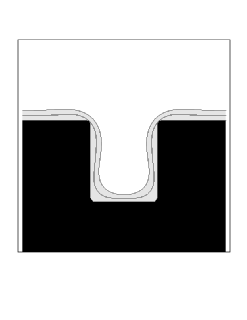
|
| Diffusion Coefficient = 0.001 | Diffusion Coefficient = 0.002 |
|

|
| Diffusion Coefficient = 0.0 | Diffusion Coefficient = 0.005 |
|
|
| Diffusion Coefficient = 0.001 | Diffusion Coefficient = 0.002 |