OVERVIEW
APPLICATIONS
INTERACTIVE APPLETS
HISTORY OF THE METHODS/FLOW CHART
PUBLICATIONS
EDUCATIONAL MATERIAL
ACKNOWLEDGEMENTS
ABOUT THE AUTHOR/CV
Copyright:
1996, 1999, 2006
J.A. Sethian
The Narrow Band Level Set Method
You are currently in the
topic outlined in red.
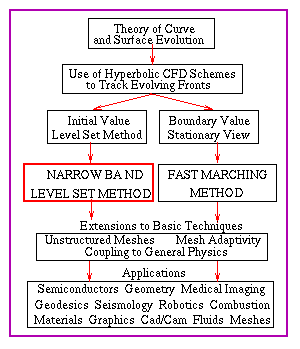
Click on navigable flow chart to go to new topic
click on any text
to go to a new topic.
|
You are currently in the topic outlined in red. |

Click on navigable flow chart to go to new topic |
click on any text to go to a new topic. |
The Narrow Band Level Set Method, introduced in Ref. 1 below, solves this problem by focusing computational energy in a thin band around the front itself. Using this approach, the operation count for the level set method drops from O(N*N) in two dimensions to O(k N), where N is the number of points in each space dimension and k is the width of the narrow band. Ref. 2 is an earlier use of this technique.
This savings is substantial; it allows three-dimensional interface evolution problems to be handled with ease.
New Book and Resource on Level Set and Fast Marching Methods
References:
-
A Fast Level
Set Method for Propagating Interfaces
: Adalsteinsson, D., and Sethian, J.A.,
Journal Computational Physics, 118, 2, pp.
269-277, 1995.
Abstract
A method is introduced to decrease the computational labor of the standard level set method for propagating interfaces. The fast approach uses only points close to the curve at every time step. We describe this new algorithm and compare its efficiency and accuracy with the standard level set approach.
Download publications
-
Computing Minimal Surfaces via Level Set Curvature
Flow
:
Chopp, D.L.
Journal of Computational Physics, 106, pp. 77-91, 1993.
Download publications