Seven Wonders of the World

The title of this section comes from an article by Richard Hoshino entitled The Other Side of Inequalities, Part Four in Mathematical Mayhem, Volume 7, issue 4, March-April 1995. Mathematical Mayhem merged with Crux Mathematicorum after Volume 8 and the two are published together by the Canadian Mathematical Society eight times a year. The cost for nonmembers is $60 a year, but a student rate of only $20 available. The article was a very successful attempt to show how some inequalities could be elegantly solved with some trigonometry. The major theme was to employ Jensen's Inequality for concave functions of three variables. Namely,

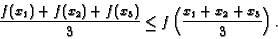$\begin{displaymath} \frac{f(x_1) + f(x_2) + f(x_3)}{3} \le f\left(\frac{x_1+x_2+x_3}{3}\right). \end{displaymath}$

(3)

Note that $f(x)=\sin x$ is concave on $[0,\pi]$ , $f(x) = \csc x$ is convex on $(0,\pi)$ , $f(x) = \cos x$ is concave on $[0,\pi/2]$ and convex on $[\pi/2,\pi]$ and $\tan x$ is convex on $(0,\pi/2)$ . As before $\alpha,\beta,$ and $\gamma$ are the angles of triangle

. The following list of inequalities comprise the Seven Wonders of the World.

[W1] $\sin\alpha+\sin\beta+\sin\gamma \le \frac{3\sqrt{3}}{2}$ .
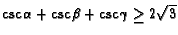
[W2] $\csc\alpha+\csc\beta+\csc\gamma \ge 2\sqrt{3}$
[W3] $1<\cos\alpha+\cos\beta+\cos\gamma \le \frac{3}{2}$ .
[W4] $\cot\alpha \cot\beta \cot\gamma \le\frac{\sqrt{3}}{9}$ .
[W5] $\cot\alpha + \cot\beta + \cot\gamma \ge \sqrt{3}$ .
[W6] $\sin^2 \alpha+\sin^2 \beta+\sin ^2 \gamma \le \frac{9}{4}$ .
[W7] $\cot^2 \alpha+\cot^2 \beta+\cot ^2 \gamma \ge 1$ .

The following are some proofs that exhibit the usefulness of Jensen's Inequality and some other standard techniques with trigonometric functions.

[W1] Since $\sin x$ is concave on $(0,\pi)$ by Jensen's Inequality we have $\frac{\sin\alpha+\sin\beta+\sin\gamma}{3} \le \sin(\frac{\alpha +\beta+\gamma}{3})$ . But $\alpha+\beta+\gamma=\pi$ , so $\frac{\alpha+\beta+\gamma}{3}=\frac{\pi}{3}$ . Multiplying both sides of the inequality by and using $\sin\frac{\pi}{ 3}= \frac{\sqrt{3}}{2}$ gives the result.
[W2] Since $\csc x$ is convex on $(0,\pi)$ by Jensen's Inequality we have
$\csc\alpha+\csc\beta+\csc\gamma \ge 3\csc[(\alpha +\beta+\gamma)/3]=3\csc\frac{\pi}{3}=2\sqrt{3}.$
[W3] If $\alpha,\beta,\gamma< \frac{\pi}{2}$ then by Jensen's Inequality we have
$\cos\alpha+\cos\beta+\cos\gamma \le 3\cos[(\alpha+\cos\beta+\cos\gamma)/3)] =\frac{3}{2}$ . Otherwise the situation becomes complicated. See Richard Hoshino's article for details. For an alternate proof see Some Harder Problems, number 3, at the end.
[W4] If one of the angles, $\alpha$ , is not acute then the value for $\cot\alpha < 0$ and the values for the other two angles will by positive so that the inequality is clearly true. If the three angles are acute, since $\tan x$ is convex and $\gamma = \pi-(\alpha +\beta)$ , we have by Jensen's Inequality $\tan\alpha+\tan\beta+\tan\gamma \ge 3 \tan[(\alpha +\beta+\gamma)/3] = 3\sqrt{3}$ . But $\tan\alpha+\tan\beta+\tan\gamma = \tan\alpha \tan\beta \tan\gamma$ (Prove this). Therefore $\tan\alpha \tan\beta \tan\gamma \ge 3\sqrt{3}$ . Taking the reciprocals we have $\cot\alpha \cot\beta \cot\gamma \le\frac {1}{3\sqrt{3}}=\frac{\sqrt{3}}{9}$ .
[W5] First note that $\cot\alpha + \cot\beta = \frac{\cos\alpha}{\sin\alpha} + \frac{\cos\beta}{\sin\... ...\alpha}{\sin\alpha \sin\beta} = \frac{\sin(\alpha+\beta)}{\sin\alpha\sin\beta}.$
But

$\begin{eqnarray*} \cos(\alpha-\beta) = \cos\alpha \cos\beta + \sin\alpha\sin\bet... ... -\cos\alpha \cos\beta + \sin\alpha\sin\beta & = & \cos\gamma\\ \end{eqnarray*}$

Adding we get

$\begin{eqnarray*} 2 \sin\alpha\sin\beta & \le & 1 + \cos\gamma\\ 2 \sin\alpha\s... ...os\gamma} & \le & \frac{\sin(\alpha+\beta)}{\sin\alpha\sin\beta} \end{eqnarray*}$

Therefore

$\begin{eqnarray*} \cot\alpha + \cot\beta + \cot\gamma & = & \frac{\sin(\alpha+\b... ...\ the\ AM\rule[1 mm]{1mm}{.2mm}GM\ Inequality}\\ & = & \sqrt{3} \end{eqnarray*}$

So $\cot\alpha + \cot\beta + \cot\gamma \ge \sqrt{3}$
[W6] Since $\gamma = \pi-(\alpha +\beta)$ and the sine of an angle equals the sine of its supplement we have $\sin^2 \alpha+\sin^2 \beta+\sin ^2 \gamma = \sin^2 \alpha+\sin^2 \beta +\sin ^2 (\alpha + \beta)$

$\begin{eqnarray*} &=& \sin^2 \alpha+\sin^2 \beta + \sin^2\alpha \cos^2\beta + 2\... ...ta\cos(\alpha+\beta)\\ &=& 2 + 2\cos\alpha\cos\beta\cos(\gamma) \end{eqnarray*}$

But from W3 we have $\frac{\cos\alpha+\cos\beta+\cos\gamma}{3}\le \frac{1}{2}$ so that $\left(\frac{\cos\alpha+\cos\beta+\cos\gamma}{3}\right)^3 \le\frac{1}{8}$ .
By the AM-GM we have $\cos\alpha\cos\beta\cos\gamma \le \left(\frac{\cos\alpha+\cos\beta+\cos\gamma}{3}\right)^3 \le \frac{1}{8}$ .
Therefore $\sin^2 \alpha+\sin^2 \beta+\sin ^2 \gamma = 2 + 2\cos\alpha\cos\beta\cos\gamma \le 2 + 2(\frac{1}{8}) = \frac{9}{4}$ .
[W7] By the AM-GM we have $\cot^2\alpha +\cot^2\beta \ge 2\cot\alpha\cot\beta$ and likewise for the other pairs. Adding the three inequalities together and dividing by 2 we have

$\begin{eqnarray*} \cot^2 \alpha+\cot^2 \beta+\cot ^2 \gamma & \ge & \cot\alpha\c... ...\\ & = & \cot\alpha\cot\beta -\cot\alpha\cos\beta+1\\ & = & 1. \end{eqnarray*}$

Therefore $\cot^2 \alpha+\cot^2 \beta+\cot ^2 \gamma \ge 1.$