Section 7.5: The method of least squares

Problem: Given a collection of data points $(x_1,y_1), \ldots, (x_n,y_n)$ find a function $y = f(x)$ which best fits these data.

Questions posed by the problem

• What kind of function should $f$ be?
• How do we measure the best fit?

Proposed answer to the first question

• The function $f$ should be defined for all real values of $x$ so that we may interpolate the data given.
• Its form should be as simple as possible so as to simplify calculations.
• The form of the function should be complicated enough to realistically model the data.

When performing linear regression one assumes that $f(x) = ax + b$ is a linear function. This assumption satisfies the first two desiderata, but seldom the last.

Proposed answer to the last question

• The function $y = f(x)$ fits the data well if size of the differences $y_i - f(x_i)$ are all small.
• We can measure the total error in many ways. For instance, we could define $E(f) = \vert y_1 - f(x_1)\vert + \cdots + \vert y_n - f(x_n)\vert = \sum_{i=1}^n \vert y_i - f(x_i)\vert$ and try to minimize this quantity. Alternatively, we could define ${\mathcal E}(f) := \max \vert y_i - f(x_i)\vert$ and try to minimize this.

Proposed answer, continued: Least squares

The methods of calculus work best with the least squares error method.

Set ${\mathcal S}(f) := (y_1 - f(x_i))^2 + \cdots + (y_n - f(x_n))^2 = \sum_{i=1}^n (y_i - f(x_i))^2$.

The equation $y = f(x)$ is a regression equation for the data if ${\mathcal S}(f)$ is minimized by $f$ among the functions of a specified class (ie linear functions).

An example of linear regression

Find the linear function having least squares error for the data $\{ (0,3), (2,4), (3,3) \}$.

Solution

Write $f(x) = ax + b$. We must solve for $a$ and $b$. We compute

$$\begin{eqnarray*} S(a,b) & := & {\mathcal S}(f) \\ & = & (3 - (a \cdot 0 + b))... ... 18a - 6b + 6ab) \\ & = & 13 a^2 + 3 b^2 + 8ab - 26a -16b + 34 \end{eqnarray*}$$

Solution, continued

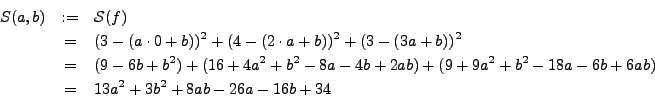
So we must minimize $S(a,b) = 13 a^2 + 3 b^2 + 8ab - 26a - 16b +34$.

Differentiating,

$$\frac{\partial S}{\partial a} = 26a + 8b - 26$$ (1)

$$\frac{\partial S}{\partial b} = 6b + 8a - 16$$ (2)

Solution, continued

Setting these equal to zero, multiplying the first equation by $3$ and the second equation by $4$, we have

$$\begin{eqnarray*} 0 & = & 78 a + 24 b - 78 \\ 0 & = & 32 a + 24 b - 48 \end{eqnarray*}$$

Subtracting, we conclude $0 = 46 a - 30$ or that $a = \frac{-15}{23} \approx -.65$. Substituting into the equation $\frac{\partial S}{\partial b} = 0$ we find $16 = 6b + 8 (\frac{-15}{23})$ so that $b = \frac{383}{138} \approx 2.8$

Solution, completed

We should test that this point is a minimum.

$$\frac{\partial^2 S}{\partial a^2} = 26$$ (3)

$$\frac{\partial^2 S}{\partial b^2} = 6$$ (4)

$$\frac{\partial^2 S}{\partial a \partial b} = 8$$ (5)

$$D_S = 92$$ (6)

$D_S > 0$ and $\frac{\partial^2 S}{\partial a^2} > 0$. Therefore, we have minimized $S$.