Section 7.3: Maxima and Minima of Functions of Several Variables
Review of Single Variable Case

If $f(x)$ is a (sufficiently differentiable) function of a single variable and $f$ has a relative minimum or maximum (generically an extremum) at $x = a$ then $f'(a) = 0$.

Recall that a function may have $f'(a) = 0$ without $a$ being an extremum.

Extrema of a Function of a Single Variable: Examples

• $f(x) = x^2 + 1$ and $a = 0$
• $g(x) = e^x - x$ and $a = 0$
• $g(x) = x^3$ and $a = 0$

Graphs

First Derivative Test for Extrema of Functions of Two Variables

If $(a,b)$ is a relative extremum of $F(x,y)$, then $a$ is a relative extremum of $g(x) := F(x,b)$ and $b$ is a relative extremum of $h(y) := F(a,y)$. So,

$$0 = g'(a) = \frac{\partial F}{\partial x} \vert_{(a,b)}$$

and

$$0 = h'(b) = \frac{\partial F}{\partial y} \vert_{(a,b)}$$

(In fact, this test applies to functions in any number of variables.)

Counterexamples

As with functions of a single variable, there may be points $(a,b)$ which are not relative extrema but for which $\frac{\partial F}{\partial x} \vert_{(a,b)} = 0 = \frac{\partial F}{\partial y} \vert_{(a,b)}$.

• $F(x,y) = x^3 y^2$
• $G(x,y) = \sin(x) \cos(y)$

Graphs

Second Derivative Test: One Variable

Recall that for a function of a single variable, one can look at the second derivative to test for concavity and thereby also the existence of a local minimum or maximum.

A (sufficiently smooth) function of one variable $f(x)$ has a relative extremum at $x = a$ if $f'(a) = 0$ and $f''(a) \neq 0$. If $f'(a) = 0$ and $f''(a) > 0$, then $a$ is a relative minimum and if $f'(a) = 0$ and $f''(a) < 0$, then $a$ is a relative maximum.

Second Derivative Test: Two Variables

Given a function $F(x,y)$ of two variables we define a new function

$$D_F(x,y) := \frac{\partial F}{\partial x} \cdot \frac{\partial F}{\partial y} - (\frac{\partial^2 F}{\partial x \partial y})$$

If

• $\frac{\partial F}{\partial x} \vert_{(a,b)} = 0 = \frac{\partial F}{\partial y} \vert_{(a,b)}$,
• $D_F(a,b) > 0$, and
• $\frac{\partial^2 F}{\partial x^2} \vert_{(a,b)} \neq 0$;

then $F$ has a relative extremum at $(a,b)$ (maximum if $\frac{\partial^2 F}{\partial x^2}\vert_{(a,b)} < 0$ and minimum if this second derivative is positive).

Second Derivative Test for Two Variables: No Extremum

Conversely, if

• $\frac{\partial F}{\partial x} \vert_{(a,b)} = 0 = \frac{\partial F}{\partial y} \vert_{(a,b)}$ and
• $D_F(a,b) < 0$;

then $F$ does not have a relative extremum at $(a,b)$.

When $D_F(a,b) = 0$, this test yields no information.

Second Derivative Test: Examples

Find the relative extrema of $f(x,y) = x^3 - y^2 - 3x + 2y$.

Graphs

Solution

$$\begin{eqnarray*} \frac{\partial f}{\partial x} & = & 3x^2 - 3 \\ \frac{\partia... ... \frac{\partial^2 f}{\partial y^2} & = & -2 \\ D_f & = & -12 x \end{eqnarray*}$$

Solution continued

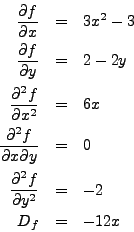
The solutions to $\frac{\partial f}{\partial x} = 0 = \frac{\partial f}{\partial y}$ are $(-1,1)$ and $(1,1)$. We compute the $D_f(-1,1) = 12 > 0$ and $D_f(1,1) = -12 < 0$. Thus, the only potential relative extremum is at $(-1,1)$.

We compute $\frac{\partial^2 f}{\partial x^2} \vert_{(-1,1)} = -6 < 0$. Thus, $(-1,1)$ is a relative maximum.

Second Derivative Test: Example 2

Find the extrema of $F(x,y) = y e^x -3x -y + 2$.

Graphs

Solution

$$\begin{eqnarray*} \frac{\partial F}{\partial x} & = & y e^x - 3 \\ \frac{\partial F}{\partial y} & = & e^x - 1 \end{eqnarray*}$$

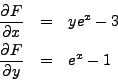
Setting both of these equal to zero, we find $x = 0$ and $y = 3$.

Solution, continued

$$\begin{eqnarray*} \frac{\partial^2 F}{\partial x^2} &=& y e^x \\ \frac{\partial... ...\partial^2 F}{\partial x \partial y} &=& e^x \\ D_F & = & -e^{2x} \end{eqnarray*}$$

As $D_F(0,3) = -1 < 0$, the point $(0,3,2)$ is not an extremum, there are no local extrema of $F$.