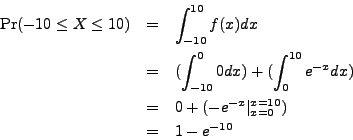Given a sequence of data points
![]() ,
its cumulative distribution function
,
its cumulative distribution function
![]() is defined by
is defined by
That is, ![]() is the relative proportion of the data points taking value
less than or equal to
is the relative proportion of the data points taking value
less than or equal to ![]() .
.
Given the data points
![]() , compute
, compute
![]() where
where ![]() is the corresponding cumulative distribution function.
is the corresponding cumulative distribution function.
There are a total of sixteen data points of which nine have a value less
than or equal to four. Thus,
![]() .
.
One may regard the cumulative distribution function ![]() as
describing the probability that a randomly chosen data point will
have value less than or equal to
as
describing the probability that a randomly chosen data point will
have value less than or equal to ![]() .
.
If ![]() is the correponding random variable, one often writes
is the correponding random variable, one often writes
From ![]() we may compute other probabilities. For instance,
the probability of obtaining a value greater than
we may compute other probabilities. For instance,
the probability of obtaining a value greater than ![]() but less than
or equal to
but less than
or equal to ![]() is
is
We may wish to express the probability that a numerical value of a particular experiment lie with a certain range even though infinitely many such values are possible.
A cumulative distribution function (in general) is a function ![]() defined for all real numbers for which
defined for all real numbers for which
We write ![]() for the corresponding random variable and treat
for the corresponding random variable and treat ![]() as
expressing
as
expressing
![]() .
.
If the cumulative distribution function ![]() (for the random variable
(for the random variable ![]() )
is differentiable and have derivative
)
is differentiable and have derivative ![]() , then we say that
, then we say that ![]() is
the probability density function for
is
the probability density function for ![]() .
.
For numbers ![]() we have
we have
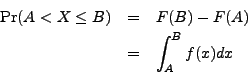
Conversely, any function satisfying the above properties is a probability density.
The function
is a probability density (for the random variable ![]() ).
).
Compute
![]() .
.
We know