A first order linear differential equation is a differential equation of the form
Solve the differential equation
In this case we can use the method of separation of variables.
If ![]() is constant, then
is constant, then
![]() so that
so that
![]() .
.
Otherwise, we may express the equation as
![]() .
Let
.
Let ![]() . Integrating with respect to
. Integrating with respect to ![]() , we have
, we have
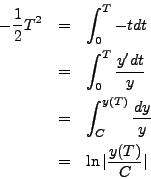
(As our solution must be continous and cannot take the value zero,
the signs of ![]() and
and ![]() must agree. So, we may
drop the absolute value bars.)
must agree. So, we may
drop the absolute value bars.)
Exponentiating both sides of this equation and multiplying by ![]() , we obtain
, we obtain
![]() .
.
Solve the differential equation
In this case, we cannot apply the separation of variables technique.
However, as ![]() is never equal to zero, the solutions to the original
equation and to the equation
is never equal to zero, the solutions to the original
equation and to the equation
are the same.
Observe that
We integrate with respect to ![]() .
.
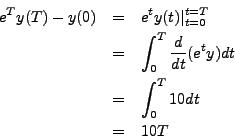
So, if we write ![]() , then we have
, then we have
![]() .
.
Solve the differential equation
In this case, multiplying by ![]() we may express the
equation as
we may express the
equation as
![]() . Using the
product rule we check that
. Using the
product rule we check that
![]() .
.
We integrate this expression.
Note: The original equation
is singular at ![]() in the sense that the function
in the sense that the function ![]() is
not defined. We need to take for the lower limit of integration
some other constant. The number
is
not defined. We need to take for the lower limit of integration
some other constant. The number ![]() is a convenient choice in this case.
is a convenient choice in this case.
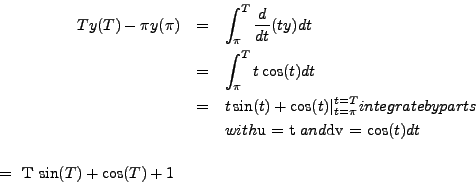
Write ![]() . Then we conclude that
. Then we conclude that
![]() .
.
In general, if ![]() , then
, then
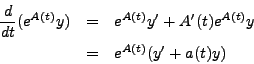
Thus, a differential equation of the form
![]() may be expressed as
may be expressed as
![]() .
.
So, if ![]() is in the domain of the functions
is in the domain of the functions ![]() and
and ![]() , we
have
, we
have
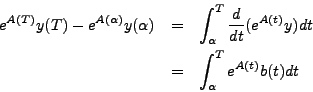
Set
![]() , then
, then
![]() .
.
In solving the equation
![]() , we multiplied by
, we multiplied by
![]() and then observed that
and then observed that
![]() .
.
In terms of the general solution,
![]() and if
and if ![]() , then
we have
, then
we have ![]() .
.
Note that
![]() . So, multiplying by
. So, multiplying by ![]() is the same
as multiplying by
is the same
as multiplying by ![]() for
for ![]() .
.
Our general method gives
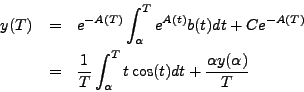
To finish, we must choose ![]() and evaluate the above integral.
and evaluate the above integral.