Section 7.1: Examples of Functions of Several Variables
A function need not be expressed in terms of a formula.
Traditionally, the variables of a function of several variables are written as
![]() or if there are more than three variables, using
subscripts
or if there are more than three variables, using
subscripts
![]() .
.
The functions themselves are usually written using symbols such a
![]() and if it is important to list the variables as, eg
and if it is important to list the variables as, eg
![]() ,
, ![]() , or
, or
![]() .
.
For function of two variables, one may graph this function by plotting the
solutions to
![]() in three space.
in three space.
Examples:
A contour map is precisely such a graph. Here the variables are the lattitude and longitude of a point on the Earth and the function gives the altitude.
(More on contour plots)
Suppose that one wishes to produce a structure in the shape of
a rectangular box. The material for the floor costs
![]() per square foot, the material for the walls costs
per square foot, the material for the walls costs ![]() per
square foot, and the material for the roof costs
per
square foot, and the material for the roof costs ![]() per square foot.
Write the total cost as a function of
per square foot.
Write the total cost as a function of ![]() , the width,
, the width, ![]() , the
length, and
, the
length, and ![]() , the height, of the structure.
, the height, of the structure.
| Area of the floor | |||
| Area of walls | |||
| Area of roof |
| Total cost | Floor cost |
||
Section 7.2: Partial Derivatives
If ![]() is a function of several variables, then for any
fixed value of
is a function of several variables, then for any
fixed value of ![]() and
and ![]() , say,
, say, ![]() and
and ![]() , the function
, the function
![]() is a function of the single variable
is a function of the single variable ![]() .
.
As such, it makes sense to compute the derivative of ![]() , or what is the
same thing, the derivative of
, or what is the
same thing, the derivative of ![]() with respect to
with respect to ![]() :
:

For a function of one variable, ![]() , the derivative of
, the derivative of ![]() at
at
![]() is defined as a limit:
is defined as a limit:
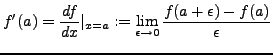
For a function of several variables, partial derivatives are defined by the same kind of limit.
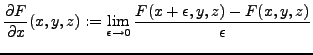
In general, to compute the partial derivative of a function with respect to some variable, treat the function as a function of that single variable with all the other named variables regarded as constants.
If ![]() is a constant and
is a constant and ![]() a natural number, then the formula
a natural number, then the formula
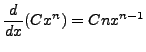
Instead, we could consider this monomial as a function of three variables
![]() (at least for
(at least for ![]() ) and the above formula
expresses
) and the above formula
expresses
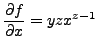
Let
![]() . Compute
. Compute
![]() ,
,
![]() , and
, and
![]() .
.
Let
![]() . Compute
. Compute
![]() and
and
![]() .
.
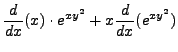 |
|||
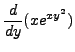 |
|||
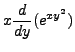 |
|||
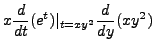 |
|||
Unlike a curve, a surface has many tangent lines at each point. The partial derivatives give the slopes of the tangent lines at a point in a specific direction.
More precisely, the partial derivative at a point ![]() of a function
of a function ![]() with respect
to
with respect
to ![]() is the slope of the tangent line to the graph
of
is the slope of the tangent line to the graph
of ![]() at
at ![]() along the direction where all coordinates
save
along the direction where all coordinates
save ![]() are held fixed.
are held fixed.
As with derivatives of a function of a single variable, partial
derivatives may be interpreted as rates of change. In this case,
![]() is the rate at which
is the rate at which ![]() changes
relative to changes in the
changes
relative to changes in the ![]() -variable with all other variables held
fixed.
-variable with all other variables held
fixed.
Let
![]() . Compute and interpret
. Compute and interpret
![]() and
and
![]() .
.
![]() . So the slope of the tangent line in the
. So the slope of the tangent line in the
![]() direction at
direction at
![]() is
is
![]() .
.
![]() . That is, the slope of the
tangent line in the
. That is, the slope of the
tangent line in the ![]() -direction is
-direction is
![]() .
.
Notice that ![]() is increasing in the
is increasing in the ![]() -direction while it is
decreasing in the
-direction while it is
decreasing in the ![]() -direction.
-direction.
A partial derivative of a function is itself a function and may be differentiated again.
It is a non-trivial, though true, theorem that for a sufficiently
smooth function the order of differentiation is immaterial. That is,
![]()
Let
![]() . Compute
. Compute
![]() ,
,
![]() and
and
![]() .
.
![]() and
and
![]() .
.
So,
![]() and
and
![]() , while
, while
![]() (or
we may compute
(or
we may compute
![]() ).
).