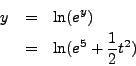The method of separation of variables applies to differential equations of the form
where ![]() and
and ![]() are functions of a single variable.
are functions of a single variable.
Find the general solution to the differential equation
Any constant solution to this equation would have
![]() so that
so that ![]() .
.
Avoiding the constant solution, we may divide both sides of the
equation by ![]() and then we solve:
and then we solve:
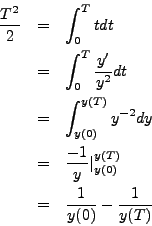
So, if we set ![]() , we have
, we have
![]() .
.
To solve the differential equation
![]() :
:
Find the general solution of
![]()
We begin by rewriting the equation at
![]() .
.
The only constant solution is ![]() .
.
Integrating, we find that ![]() is an antiderivative of
is an antiderivative of
![]() while
while ![]() is an antiderivative of
is an antiderivative of ![]() .
.
Let ![]() . Then we have
. Then we have
![]() .
.
Adding ![]() to both sides and applying the exponential function,
we conclude that
to both sides and applying the exponential function,
we conclude that
![]() .
.
As the solution ![]() must be continuous, the signs of
must be continuous, the signs of ![]() and
and ![]() agree. Thus,
agree. Thus,
![]() .
.
Note: In this case the constant solution has the same form.
Find the general solution to the differential equation
![]()
The method of separation of variables does not apply as the function
![]() cannot be written as the product of a function of
cannot be written as the product of a function of ![]() by a function of
by a function of ![]() .
.
Scholium: Using Taylor series expansions (a topic which
we shall discuss next month), one can compute an expression
for solutions to the equation ![]() .
.
Find the general solution to the equation
There are no constant solutions as
![]() is never zero.
Note, however, that we cannot have
is never zero.
Note, however, that we cannot have ![]() as the differential
equation would require
as the differential
equation would require ![]() to be nondifferentiable at such a point.
to be nondifferentiable at such a point.
As before, we set ![]() . Multiplying by
. Multiplying by ![]() and integrating,
we find
and integrating,
we find
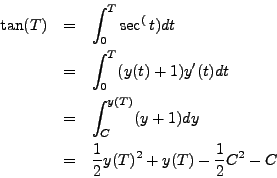
So, ![]() satisfies the equation
satisfies the equation
From the quadratic formula, we compute that
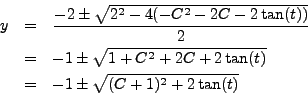
Find a function ![]() satisfying
satisfying ![]() and
and
![]() .
.
As the exponential function never attains the value zero, there are
no constant solutions to this differential equation. Multiplying both
sides of the equation by ![]() and integrating, we obtain:
and integrating, we obtain:
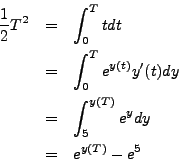
Addding ![]() to both sides of this equation and taking the natural logarithm, we
compute
to both sides of this equation and taking the natural logarithm, we
compute