Section 9.6: Improper integrals

We have considered only integrals of the form $\int_a^b f(x) dx$ where $a \leq b$ are real numbers and $f$ is a function which is defined and continuous on the interval $[a,b] := \{ x ~\vert~ a \leq x \leq b \}$.

Sometimes, it makes sense to consider integrals over infinite intervals and for functions that are discontinuous or not necessarily defined at every point in the interval.

Example

What sense can we make of $\int_0^\infty e^{-x} dx$?

A solution

The function $f(x) = e^{-x}$ is positive for every value of $x$. Thus, $\int_0^\infty e^{-x} dx$ ought to be the area of the region bounded by the graph of $y = e^{-x}$, the $y$-axis, and the $x$-axis.

This region is eventually covered by the regions bounded by $y = e^{-x}$, the $y$-axis, $x$-axis, and the line $x = r$ for $r$ a sufficiently large real number.

In this case, $\int_0^\infty e^{-x} dx = \lim_{r \to \infty} \int_0^r e^{-x} dx = \lim_{r \to \infty} [-e^{-x} \vert_0^r] = \lim_{r \to \infty} [-e^{-r} + 1] = 1$.

Integration over infinite intervals

If $a$ is a real number and $f$ is a function which is continuous on the interval $[a,\infty) = \{ x ~\vert~ a \leq x \}$, then we define $\int_a^\infty f(x) dx = \lim_{r \to \infty} \int_a^r f(x) dx$.

Nota Bene: This limit might not exist!

Example

Compute $\int_0^\infty \sin(x) dx$.

Solution

$$\begin{eqnarray*} \int_0^\infty \sin(x) dx & = & \lim_{r \to \infty} -\cos(x) \v... ... (-\cos(r) + \cos(0)) \\ & = & 1 - \lim_{r \to \infty} \cos(r) \end{eqnarray*}$$

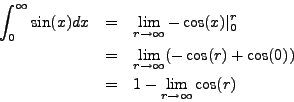
This limit does not exist! For each value of $r$, there are $s$ and $t$ bigger than $r$ with $\cos(s) = 1$ and $\cos(t) = -1$ (take $s$ to be an even multiple of $\pi$ and $t$ an odd multiple of $\pi$).

Another example

Compute $\int_1^\infty \frac{dx}{x}$.

Solution

$$\begin{eqnarray*} \int_1^\infty \frac{dx}{x} & = & \lim_{r \to \infty} [\ln(x) \... ... \ln(1)] \\ & = & \lim_{r \to \infty} \ln(r) \\ & = & \infty \end{eqnarray*}$$

Yet another example

Compute $\int_2^\infty \frac{dx}{x (\ln(x))^2}$.

Solution

Via the change of variables $u = \ln(x)$ (with $du = \frac{dx}{x}$), we see that

$$\begin{eqnarray*} \int \frac{dx}{x (\ln(x))^2} & = & \int u^{-2} du \\ & = & \frac{-1}{u} + C \\ & = & \frac{-1}{\ln(x)} + C \end{eqnarray*}$$

Solution, continued

Thus,

$$\begin{eqnarray*} \int_2^\infty \frac{dx}{x (\ln(x))^2} & = & \lim_{r \to \inf... ...rac{-1}{\ln(r)} - \frac{-1}{\ln(2)}) \\ & = & \frac{1}{\ln(2)} \end{eqnarray*}$$

Integrals over the real line

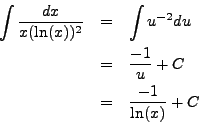
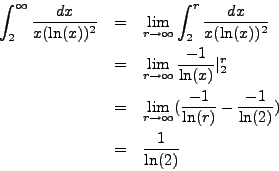
Analogously to integrals of the form $\int_a^\infty f(x) dx$, we define $\int_{-\infty}^a f(x) dx := \lim_{r \to -\infty} \int_r^a f(x) dx$. If this limit does not exist, then we say that the integral is undefined.

We define $\int_{-\infty}^\infty f(x) dx := \int_{-\infty}^0 f(x) dx + \int_0^\infty f(x) dx$.

A warning

Nota Bene: There are two separate limits involved in the definition of $\int_{-\infty}^\infty f(x) dx$. Namely,

$$\int_{-\infty}^\infty f(x) dx = (\lim_{r \to -\infty} \int_r^0 f(x) dx) + (\lim_{s \to \infty} \int_0^s f(x) dx)$$

If the limits defining $\int_{-\infty}^\infty f(x) dx$ exist, then

$$\int_{-\infty}^\infty f(x) dx = \lim_{r \to \infty} \int_{-r}^r f(x) dx$$

However, the limit on the righthand side of this equation may exist without $\int_{-\infty}^\infty f(x) dx$ being defined.

Example

Compute $\int{-\infty}^\infty x dx$.

Solution

$$\begin{eqnarray*} \int_0^\infty x dx & = & \lim_{r \to \infty} \int_0^r x dx \\ ... ...m_{r \to \infty} \frac{1}{2} r^2 \\ & \text{\lq\lq $=$''} & \infty \end{eqnarray*}$$

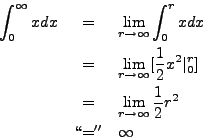
That is, the limit does not exist. Therefore, $\int_{-\infty}^\infty x dx$ is undefined.

However, $\lim_{r \to \infty} \int_{-r}^r x dx = \lim_{r \to \infty} [\frac{1}{2} x^2\vert_{-r}^r] = \lim_{r \to \infty} [\frac{1}{2} r^2 - \frac{1}{2} (-r)^2] = 0$.

Vertical asymptotes

If $f(x)$ is continuous for $a < x \leq b$, then we define $\int_a^b f(x) dx := \lim_{r \to a} \int_r^b f(x) dx$. When $f$ is continuous at $a$ as well, then this definition agrees with the old definition.

Example

Compute $\int_0^4 \frac{dx}{\sqrt{x}}$.

Solution

$$\begin{eqnarray*} \int_0^4 \frac{dx}{\sqrt{x}} &= & \int_0^4 x^\frac{-1}{2} dx \... ...ert_r^4] \\ & = & \lim_{r \to 0} [4 - 2 \sqrt{r}] \\ & = & 4 \end{eqnarray*}$$