If at time ![]() the rate of income generated by some enterprise
is given by the value of the function
the rate of income generated by some enterprise
is given by the value of the function ![]() , then the
total income generated between time
, then the
total income generated between time ![]() and time
and time ![]() is
is
![]() .
.
What value should one assign to an expected future payment?
Recall that if one has a principal of ![]() which earns
continuously compounded interest at a rate of
which earns
continuously compounded interest at a rate of ![]() , then
after
, then
after ![]() years, the investment would be worth
years, the investment would be worth ![]() .
.
The present value of a payment of $![]() made
made ![]() years in the future is the
amount
years in the future is the
amount ![]() for which with a principal of $
for which with a principal of $![]() dollars invested for
dollars invested for ![]() years
with continuously compounded interest of rate
years
with continuously compounded interest of rate ![]() one would earn $
one would earn $![]() .
.
From the formula for continuously compounded interest, we conclude
that ![]() so that
so that ![]() .
.
Suppose that some enterprise produces income at a steady rate of
$![]() per year. Of course, this income stream over the next
per year. Of course, this income stream over the next ![]() years will produce $
years will produce $![]() , but how much is it worth in present dollars?
, but how much is it worth in present dollars?
We may approximate the continous income stream as one that is paid in discrete increments.
Suppose that between now and ![]() years from now
years from now ![]() payments
are made at uniform intervals. Then, the length of time between
each payment is
payments
are made at uniform intervals. Then, the length of time between
each payment is
![]() years.
years.
The ![]() payment of
payment of ![]() is made at time
is made at time ![]() .
As such, if we assume an interest rate of
.
As such, if we assume an interest rate of ![]() , it has a present
value of
, it has a present
value of
![]() .
.
So, the sum of the present values is
![]() .
.
The expression
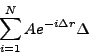
is the right-hand approximation to
Assuming an interest rate of ![]() %, compute the present value of a constant
income stream of $
%, compute the present value of a constant
income stream of $![]() per year for
per year for ![]() years.
years.
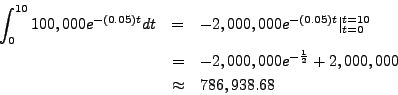
If the income stream varies as a function of time, so that at
time ![]() ,
, ![]() is the rate at which the payments are made, and
the interest rate also varies (possibly) as a function of time,
given by the function
is the rate at which the payments are made, and
the interest rate also varies (possibly) as a function of time,
given by the function ![]() , then the present value of the
income stream over the next
, then the present value of the
income stream over the next ![]() years is
years is
Suppose the interest rate is constantly
![]() % and the income stream is given by the
function
% and the income stream is given by the
function
![]() . What is the present value of
this income stream over the next
. What is the present value of
this income stream over the next ![]() years?
years?
We compute that
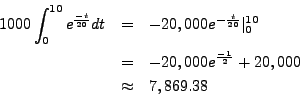
Integrating by parts, with ![]() and
and
![]() , so that
, so that
![]() and
and
![]() .
.
So,
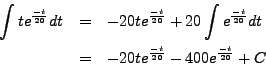
Thus,
![]() .
.
So, the total present value is
![]() .
.