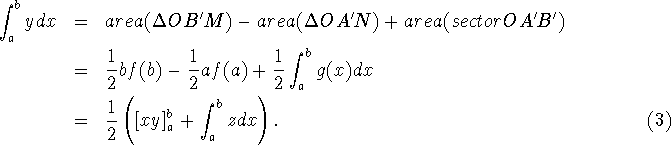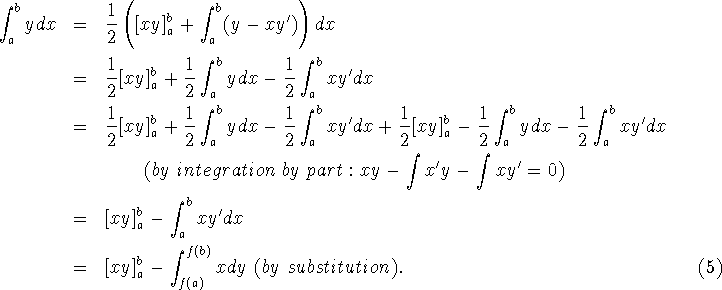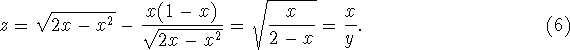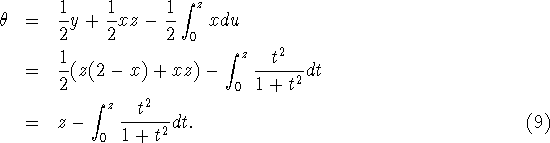
---

| Short Biography | Early Journey in Mathematics | Work | Bibliography | Back to the front page

Work
Jimmy Iskandar

David Eugene Smith says

Clearly we are indebted to him for the following contributions to the development of calculus:

1. He invented a convenient symbolism.
2. He enunciated definite rules of procedure which he called algorithms.
3. He realized and taught that quadratures constitute only a special case of integration; or, as he then called it, the inverse method of tangents.
4. He represented transcendental lines by means of differential equations (619).

However, only his first great achievement in mathematics, which coincides with point 3 above, will be discussed here by employing the same ideas but using a modern symbolism, especially the notations for differential and integral that he invented later (note: most of the calculations performed here are adopted from the Ranjan Roy's article, and to know more about this article, please consult the bibliography at the back). His first great achievement was the discovery of the series for , which took place in Paris in 1674 just after two years of his serious study in mathematics. The series for was obtained from applying the transmutation theorem to the quadrature of a circle. The idea behind the theorem, which he obtained from the study of Pascal, is that suppose P and Q are areas and they are divided up into indivisibles represented by infinitesimal triangles or rectangles. P and Q have equal areas if the area of the indivisibles of P is equal to the area of the indivisibles of Q, and there is a one-to-one correspondence between the indivisibles of P and the indivisibles of Q [Roy, 293].

He obtained the transformation formula while he divided up an area into triangles.

Let AC be the straight line tangent to y=f(x), OD be the straight line drawn perpendicular to AC, and ABE be an infinitesimal triangle with ds, dx and dy as its sides. He showed that area( ) = 1/2 area(rectangle PQRS). Noticing that is similar to , he showed that

Thus,

Now, if the point B moves along the curve y=f(x) and let the point P move together with the point B, then the curve z=g(x) is formed. Let the sector denote the region closed by y=f(x), the straight line and . Thus, by (1) Leibniz discovered the transmutation formula.

As a consequence, the area under y=f(x) can be computed as follow

Since

the formula (3) can be rewritten as

This is the Leibniz's transmutation theorem.

Now if y=f(x) is a circle of radius 1 and center (1,0), . By equation(4),

Let the semicircle with equation be drawn,

The second area can be expressed as

Now, by the transmutation theorem,

Then,

Since and by (6) ,

Further, he used the method which Nicolaus Mercator had written the infinite series for to solve the hyperbole quadrature problem. The infinite series for is

By similar argument to Mercator, he showed that

and

Hence,

This series is the , since and . In particular, if x=y then z=1 and thus Leibniz found the series for .